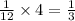Question

Tanya prepared 4 different letters to be sent to 4 different addresses. For each letter, she prepared an envelope with its correct address. If the 4 letters are to be put into the 4 envelopes at random, what is the probability that only 1 letter will be put into the envelope with its correct address?A. 1/24B. 1/8C. 1/4D. 1/3E. 3/8

Answer 1

1/3 is the answer.

Explanation:

Tanya prepared 4 different letters to be sent to 4 different addresses.

To solve this we can do the following:

The probability that the 1st letter is in the right envelope is =
`(1)/(4)`

The probability that the 2nd letter is in the wrong envelope is =
`(2)/(3)`

The probability that the 3rd letter is in the wrong envelope is =
`(1)/(2)`

The probability that the 4th letter is in the wrong envelope is = 1

So, the answer becomes:
`(1)/(4)* (2)/(3)* (1)/(2)*1` =
`(1)/(12)`

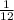
As we need 4 correct letters in the envelope, we will multiply by 4:

`(1)/(12)*4=(1)/(3)`