Question

A study claims that college students spend an average of 4 hours or less studying per day. A researcher wants to check if this claim is true. A random sample of 121 college students randomly selected and it showed that average of hours studying per day was 3.15 with a standard deviation of 1.2 hours. Using the 10% significance level, can you conclude that the claim college students spend an average of 4 hours or less studying per day is valid?

1. H0 hypothesis: A. μ > 4 B. μ ≥ 4 C.μ ≤ 4 D. μ < 4
2. Critical Value: A. -1.28 B. 1.28 C. 1.645 D. -1.645
3. Test statistics: A. -5.89 B. 5.89 C. -7.79 D. 7.79
4. Comment: A: Accept that college students spend an average of 4 hours or less studying per day
B:Reject that college students spend an average of 4 hours or less studying per day

Answer 1

n = 121

x = 3.15

`\sigma = 1.2`

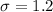
Since we are given that the claim is college students spend an average of 4 hours or less studying per day is valid

Null hypothesis :
`H_0: \mu>4`

Alternate hypothesis:
`H_a:\mu\leq 4`

1)
`H_0: \mu>4`

Now we are given that significance level is 10%

So, confidence interval is 90%

Critical value at 90% is 1.645

2)Critical value : B : 1.645

Since n >30

So we will use z test

Now we are supped to calculate z statistics

Formula :
`z=(x-\mu)/((\sigma)/(√(n)))`

`z=(3.15-4)/((1.2)/(√(121)))`

`z=-7.79`

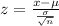
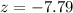
3)So, Test statistics: C. -7.79

Since the z value falls in the critical region

So, we reject the null hypothesis

So, that college students spend an average of 4 hours or less studying per day

4) A: Accept that college students spend an average of 4 hours or less studying per day