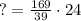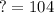Question

Find the missing length with Mark with a question mark. part 2

​

Answer 1

104

Explanation:

It tells us the triangles are similar because of the ~.

The order matters in this statement: RST~RED.

It tells us which sides are proportional:

`(RS)/(RE)=(ST)/(ED)=(TR)/(DR)`

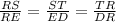
So we are given DR=39 and ER=24 and RT=169.

Let's see which part of our equation we wrote that we can use.

Note: RT is same as TR. ER is same as RE.

We are using first and the last fraction of what I wrote:

`(SR)/(ER)=(RT)/(RD)`

`(?)/(24)=(169)/(39)`

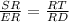
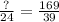
To solve for ? just multiply both sides by 24:

`?=(169)/(39)\cdot 24`

`?=104`

Answer 2

104

Explanation:

You have to be careful with this one, as the picture is misleading.

RS/RT = RE/RD . . . . . . . corresponding sides are proportional

RS/169 = 24/39 . . . . . . . fill in the given values

RS = 169·24/39 = 104