Question

A trash company is designing an​ open-top, rectangular container that will have a volume of 3645 ft cubed. The cost of making the bottom of the container is​ $5 per square​ foot, and the cost of the sides is​ $4 per square foot. Find the dimensions of the container that will minimize total cost.

Answer 1

Answer:L=9.3 ft

b=9.3 ft

h=42.14 ft

Explanation:

Given

volume(V)=
`3645 ft^3`

let L,b,h be length ,breadth and height of cube

Bottom cost
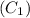`(C_1)`=5Lb

Side Costs
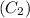`(C_2)`=8Lh+8bh

Total cost(C)=5Lb+8Lh+8bh

C=
`5* (3645)/(h)+8h\left ( L+b\right )`

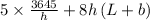
considering to be fixed ,cost become the function of L+b

and if h is fixed then Lb is also fixed and for cost to be minimum L+b should be minimum therefore L=b is necessary

thus
`b^2=(3645)/(h)`

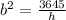
C=
`5b^2+(16* 3645)/(b)`

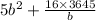
For minimum cost differentiate w.r.t b

`\frac{\mathrm{d}C}{\mathrm{d} b}=10b-(16* 3645)/(b)`

`\frac{\mathrm{d}C}{\mathrm{d} b}=0`

`10b-(16* 3645)/(b)=0`

`b=9.29\approx 9.3 ft`

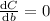
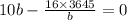
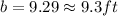
L=9.3 ft

h=42.14 ft