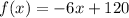Answer:
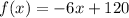
Explanation:
Let's call y the number of patients treated each week
Let's call x the week number.
If the reduction in the number of patients each week is linear then the equation that models this situation will have the following form:

Where m is the slope of the equation and b is the intercept with the x-axis.
If we know two points on the line then we can find the values of m and b.
We know that During week 5 of flu season, the clinic saw 90 patients, then we have the point:
(5, 90)
We know that In week 10 of flu season, the clinic saw 60 patients, then we have the point:
(10, 60).
Then we can find m and b using the followings formulas:
 and
and
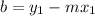
In this case:
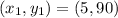 and
and
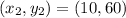
Then:
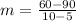
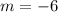
And
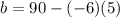
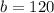
Finally the function that shows the number of patients seen each week at the clinic is: