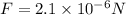Question

A microwave oven operates with sinusoidal microwaves at a frequency of 2400 MHz. The height of the oven cavity is 25 cm and the base measures 30 cm by 30 cm. Assume that microwave energy is generated uniformly on the upper surface of the cavity and propagates directly downward toward the base. The base is lined with a material that completely absorbs microwave energy. The total microwave energy content of the cavity is 0.50 µJ. What magnitude force does the microwave beam exert on the base of the oven?

Answer 1

`F=2.1* 10^(-6) N`

Step-by-step explanation:

From the problem we have

`f=2400MHz\\h=25cm\\A_(base)=(30 * 30) cm\\E=0.5 \mu J`

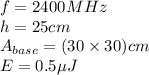
Where
`f` is frequency,
`h` is height,
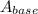`A_(base)` and
`E` is the microwave energy.

First of all, we need to tranform length units to meters. In the case of the heigh, we just have to divide by 100, because 1 meter equals 100 centimeters:

`h=25cm (1m)/(100cm)=0.25m`

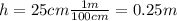
Then, the area of the base would be

`A_(base)=(30 * 30) cm^(2) =900 cm^(2) (1m^(2) )/((100cm)^(2) )=0.09m^(2)`

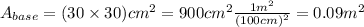
Now, to find the force exterted on the base of the oven, we first need to find the radiation pressure. But, before that, we need to know the intensity, and to find it, we need to first calculate the power, which is defined as

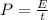`P=(E)/(t)` Where
`P` is the power,
`E` is the energy and
`t` is the time.

Replacing all values, we have

`P=(E)/(t)=(0.5 * 10^(-6) )/(t)`

As you can see, we need to find the time of the movement of the microwave beam, wich is can be found using constant kinematics

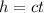`h=ct` where
`c` is the speed of the light (we are talking about an electromagentic wave),
`h` is the height (the distance that the beam will travel), and
`t` is the time of the movement.

Also, we know that

`c=3 * 10^(8) m/s`

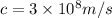
Replacing all values, we find the time

`h=ct\\t=(h)/(c)=(0.25m)/(3* 10^(8) m/s)=0.08* 10^(-8)s=8* 10^(-10)s`

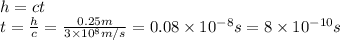
Now, we can find the power

`P=(E)/(t)=(0.5 * 10^(-6) J)/(8* 10^(-10)s )=0.0625* 10^(5) W=625W`

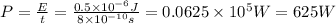
Then, we calculate the intensity

`I=(P)/(A)\\ I=(625W)/(0.09m^(2) )=6944.44 W/m^(2)`

Now, the radiation pressure

`P_(r) =(I)/(c) =(6944.44W)/(3* 10^(8) m/s) =2314.81* 10^(-8)=2.31* 10^(-5)`

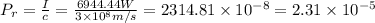
Lastly, using this radiation pressure we can find the force that cause it

`P_(r) =(F)/(A) \\F=P_(r)A=2.31* 10^(-5) (0.09m^(2))=0.21* ^(-5) N=2.1* 10^(-6) N`

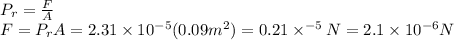
Therefore, the force exterted on the base of the oven is

`F=2.1* 10^(-6) N`

Answer 2

F = 2 × 10⁻³ N

Step-by-step explanation:

Given:

frequency, f = 2400 MHz

Height, h = 25cm = 0.25 m

Area of the base, A = 30 cm x 30 cm = 900 cm² = 0.09 m²

Energy of the microwave, E = 0.50 mJ = 0.5 x 10⁻³ J

Now, the time taken by the wave from top to the base, t = h/c

here, c is the speed of the light

thus,

t = 0.25/(3 x 10⁸) = 8.33 x 10⁻¹⁰ s

The radiation pressure
`P_r` = Intensity/c

now, the intensity is given as:

I = Power/ area

also,

Power = Energy/ time = 0.5 x 10⁻³ J/8.33 x 10⁻¹⁰ s = 600000 W

thus,

I = 600000 W/ 0.09 m² = 6666666.6 W/m²

substituting the value in the formula for pressure due to radiation, we have

`P_r` = 6666666.6 W/m²/(3 x 10⁸)

also

pressure = Force/ area

thus,

Force/ area = 6666666.6 W/m²/(3 x 10⁸)

or

Force (F) = (6666666.6 W/m² × 0.09 m²)/(3 x 10⁸)

or

F = 2 × 10⁻³ N