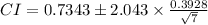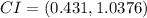Answer:
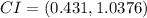
Step-by-step explanation:
Given that:
The sample size , n = 7
The mean of the observation:
Mean = Sum of observation / Total number of observation
= (0.56+ 0.72+ 0.10 + 0.99 + 1.32 + 0.52 + 0.93) / 7 = 0.7343
The standard deviation:
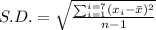
Calculating SD as:

SD = 0.3928
Degree of freedom = n-1 = 6
The critical value for t at 2% level of significance and 6 degree of freedom is 2.043.
So,
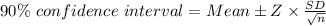
So, applying values , we get: