Question

Determine whether a figure with the given vertices is a parallelogram. Use the method indicated.

A(4, 5), B(–7, –10), C(–4, –9), D(7, 6); Distance and Slope Formulas
Question 15 options:

Yes; The opposite sides are congruent and have the same slope.

Yes; The opposite sides have the same slope.

No; The opposite sides have the same slope.

No; The opposite sides are congruent and have the same slope.

Answer 1

Answer with explanation:

The coordinates of four points of Quadrilateral ABCD are

A(4, 5), B(–7, –10), C(–4, –9), D(7, 6)

`AB=√((4+7)^2+(5+10)^2)\\\\AB=√(121+225)\\\\AB=√(346)\\\\BC=√((-7+4)^2+(-10+9)^2)\\\\BC=√(9+1)\\\\BC=√(10)\\\\CD=√((4+7)^2+(5+10)^2)\\\\CD=√(121+225)\\\\CD=√(346)\\\\DA=√((7-4)^2+(6-5)^2)\\\\DA=√(9+1)\\\\DA=√(10)`

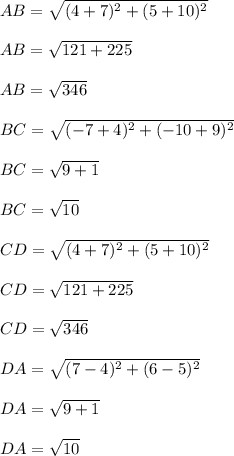
Slope between two points is given by

`m=(y_(2)-y_(1))/(x_(2)-x_(1))\\\\m_(1)=(-10-5)/(-7-4)\\\\=(-15)/(-11)\\\\m_(1)=(15)/(11)\\\\m_(2)=(-9+10)/(-4+7)\\\\m_(2)=(1)/(3)\\\\m_(3)=(6+9)/(7+4)\\\\m_(3)=(15)/(11)\\\\m_(4)=(6-5)/(7-4)\\\\m_(4)=(1)/(3)`

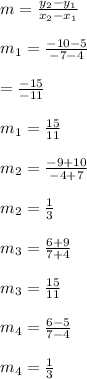
As slope of opposite sides are equal and length of Opposite sides are equal.So,the given Quadrilateral is a Parallelogram.

Option A

Yes; The opposite sides are congruent and have the same slope.