check the links in the comments above, notice on all those links, we multiply top and bottom always by the same value, it being the conjugate pair or just a rational or something else, is the same value atop and below.
now, what is same over same?
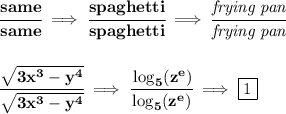
so you see, we're really always multiplying the fraction by 1, so its top and bottom are just 1 in disguise.