Answer:
k = 30
Explanation:
The formula for the mean is:
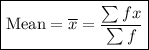
where:
- x = data value
- f = frequency of each x
Given:
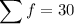
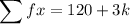
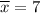
Substitute the given values into the formula and solve for k:
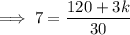
Multiply both sides by 30 to eliminate the denominator on the right side:
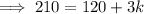
Subtract 120 from both sides:
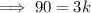
Divide both sides by 3:
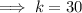
Therefore, k = 30.