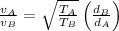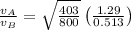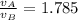Question

Two steel guitar strings have the same length. String A has a diameter of 0.513 mm and is under 403 N of tension. String B has a diameter of 1.29 mm and is under a tension of 800 N. Calculate the ratio of the wave speeds, vA/vB, in these two strings.

Answer 1

`(v_(A))/(v_(B)) = 1.785`

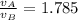
Step-by-step explanation:

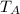`T_(A)` = Tension force in string A = 403 N

`T_(B)` = Tension force in string B = 800 N

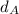`d_(A)` = diameter of string A = 0.513 mm

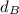`d_(B)` = diameter of string B = 1.29 mm

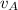`v_(A)` = wave speed of string A

`v_(B)` = wave speed of string B

Ratio of the wave speeds is given as

`(v_(A))/(v_(B)) = \sqrt{(T_(A))/(T_(B))} \left ( (d_(B))/(d_(A)) \right )`

`(v_(A))/(v_(B)) = \sqrt{(403)/(800)} \left ( (1.29)/(0.513) \right )`

`(v_(A))/(v_(B)) = 1.785`