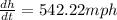Question

A plane flying horizontally at an altitude of 1 mi and a speed of 560 mi/h passes directly over a radar station. Find the rate at which the distance from the plane to the station is increasing when it is 4 mi away from the station. (Round your answer to the nearest whole number.)

Answer 1

Given:

altitude, x = 1 mile

speed, v = 560 mi/h

distance from the station, x = 4 mi

Solution:

To find the rate,

`(dx)/(dt) = 0`

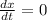
Now, from the right angle triangle in fig 1.

Applying pythagoras theorem:

`h^(2)=x^(2) + y^(2)`

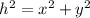
differentiating the above eqn w.r.t 't' :

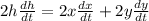`2h(dh)/(dt) = 2x(dx)/(dt) + 2y(dy)/(dt)` (1)

Now, putting values in eqn (1):

`2h(dh)/(dt) = 2* 1* 0 + 2y(dy)/(dt)`

`(dh)/(dt) = (y)/(h)(dy)/(dt)`

`(dh)/(dt) = (560)/(4)(dy)/(dt)`

`(dh)/(dt) = (560)/(4)(dy)/(dt)`

`(dh)/(dt) = 140√(4^2 - 1)`

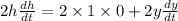
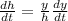
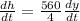
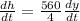
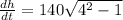
The rate at which distance from plane to station is increasing is:

`(dh)/(dt) = 542.22 mph`