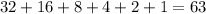Answer:
A regional soccer tournament has 64 participating teams.
In the first round of the tournament, 32 games are played.
In each successive round, the number of games played decreases by 1/2.
Part A:
We know;

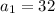
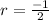
So, we get;
The rule for the number of games played in the nth round is given by:

where
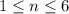
Part B:
As in each successive round the rounds are decreasing by 1/2 we have.
round 1 = 32
round 2 = 16
round 3 = 8
round 4 = 4
round 5 = 2
round 6 = 1
So, the total number of games played in the regional soccer tournament are: