Answer:
Step-by-step explanation:
a)
d = separation of the slits = 0.30 mm = 0.30 x 10⁻³ m
λ = wavelength of the light = 496 nm = 496 x 10⁻⁹ m
n = order of the bright fringe
D = screen distance = 130 cm = 1.30 m
 = Position of nth bright fringe
= Position of nth bright fringe
Position of nth bright fringe is given as
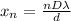
For n = 1
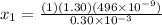

For n = 2

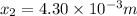
For n = 3

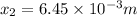
b)
Position of nth dark fringe is given as
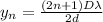
For n = 1


For n = 2
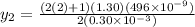
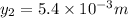
For n = 3

