Question

A vertical spring with spring constant 23.15 N/m is hanging from a ceiling. A small object is attached to the lower end of the spring, and the spring stretches to its equilibrium length. The objects is then pulled down a distance of 19.79 cm and released. The speed of the object at a distance 7.417 from the equilibrium point is 0.7286 m/s. What is the mass of the object?

Answer 1

m= 1.47 kg

Step-by-step explanation:

Given:

spring constant, K = 23.15 N/m

Displacement, x= 19.79 cm = 0.1979 m

at, x₁= 7.417 cm, v₁= 0.7286 m/s

Now,

x = 19.79 cos ( ωt)

on substituting the values, we get

7.417 x 10⁻² = 19.79 x 10⁻² cos (ωt)

or

cos(ωt) = 0.374

or

ωt = 67.98°

also

v = -0.1979×ωsin (ωt)

also

`\omega=(2\pi)/(T)`

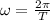
on substituting the values in the above equation, we get

0.7286 = -0.1979
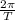`(2\pi)/(T)` sin ( 67.98°)

3.68 =-
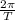`(2\pi)/(T)`(0.927)

or

T = 1.582 sec

also,

`T=2\pi\sqrt{(m)/(k)}`

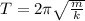
where, m is the mass

on substituting the values, we have

`1.582=2\pi\sqrt{(m)/(23.15)}`

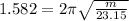
on squaring both sides and solving, we have

m= 1.47 kg