Question

Find a fundamental set of solutions for the system: x' = (2 0 3 4)x

Answer 1

The fundamental set of solutions are:

`x_1=Ae^(2t)`

`x_2=B`

`x_3=Ce^(3t)`

`x_4=De^(4t)`

Hence, the fundamental set of solutions are:

`\{e^(2t),B,e^(3t),e^(4t)\}`

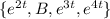
Explanation:

We are given a set as:

`x'=(2\ \ 0\ \ 3\ \ 4)x`

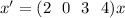
which in matrix form could be given by:

`\left[\begin{array}{ccc}x_1'\\x_2'\\x_3'\\x_4'\end{array}\right]=[2\ \ 0\ \ 3\ \ 4]\left[\begin{array}{ccc}x_1\\x_2\\x_3\\x_4\end{array}\right]`

Now, this could also be written in the form:

`\left[\begin{array}{ccc}x_1'\\x_2'\\x_3'\\x_4'\end{array}\right]=\left[\begin{array}{ccc}2\cdot x_1\\0\cdot x_2\\3\cdot x_3\\4\cdot x_4\end{array}\right]\\\\i.e.\\\\\left[\begin{array}{ccc}x_1'\\x_2'\\x_3'\\x_4'\end{array}\right]=\left[\begin{array}{ccc}2x_1\\0\\3x_3\\4x_4\end{array}\right]`

Now, in order to find each of the x_i's we have:

`x_1'=2x_1\\\\i.e.\\\\(x_1')/(x_1)=2\\\\\text{on\ integrating\ both\ side\ we\ have}\\\\\log x_1=2t+c\\\\\text{where\ c\ is\ a\ constant}\\\\x_1=e^(2t+c)\\\\i.e.\\\\x_1=e^(2t)e^c\\\\i.e.\\\\x_1=Ae^(2t)`

where A is a constant.

Similarly we have:

`x_2'=0\\\\i.e.\\\\\text{on\ integrating\ both\ side\ we\ have}\\\\x_2=B`

where B is a constant.

`x_3'=3x_3`

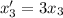
As done for x_1 we have:

`x_3=Ce^(3t)`

and

`x_4'=4x_4`

Hence,

`x_4=De^(4t)`