Use the encrypting congruence c ≡ (7p + 12) mod 26 to code the message PARALLEL LINES.

Question

asked Jan 26, 2020 148k views

1 Answer

Rbrown · Answer 1 · 2020-02-02T11:11:54+0000

Answer: PARALLEL LINES should be coded as "TSHSRRUR RWFUO"

Explanation:

Since we have given that

PARALLEL LINES

As we know that according to alphabets,

P is at 16

A is at 1

R is at 18

L is at 12

E is at 5

N is at 14

S is at 19

And we have given that

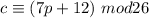
$c \equiv(7p+12)\ mod 26$

So, P becomes :

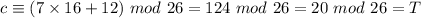
$c\equiv (7* 16+12)\ mod\ 26=124\ mod\ 26=20\ mod\ 26=T$

A becomes

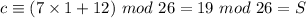
$c\equiv (7* 1+12)\ mod\ 26=19\ mod\ 26=S$

S becomes

$c\equiv (7* 19+12)\ mod\ 26=145\ mod\ 26=15\ mod\ 26=O$

L becomes

$c\equiv (7* 12+12)\ mod\ 26=96\ mod\ 26=18\ mod\ 26=R$

E becomes

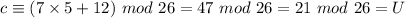
$c\equiv (7* 5+12)\ mod\ 26=47\ mod\ 26=21\ mod\ 26=U$

I becomes

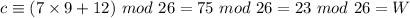
$c\equiv (7* 9+12)\ mod\ 26=75\ mod\ 26=23\ mod\ 26=W$

N becomes

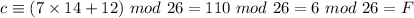
$c\equiv (7* 14+12)\ mod\ 26=110\ mod\ 26=6\ mod\ 26=F$

R becomes

$c\equiv (7* 18+12)\ mod\ 26=138\ mod\ 26=8\ mod\ 26=H$

Hence, PARALLEL LINES should be coded as "TSHSRRUR RWFUO"