Question

Initial value problem

d2y/dx2-3xdy/dx+2x=0, x0=6 d2y/dx2=-5
(i) Solve the problem using the standard form of the general solution, based on the characteristic
equation.
(ii) Solve the problem as a system of rst order ODEs, by letting y1 = X and y2 = y01

Answer 1

Since you explicitly mention "characteristic equation", I assume you mean the differential equation is

`(d^2y)/(dx^2) - 3(dy)/(dx) + 2y = 0`

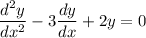
because the phrase is often used in the context of linear ODEs with constant coefficients.

The characteristic equation is then

`r^2 - 3r + 2 = (r - 2) (r - 1) = 0`

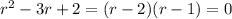
with roots
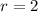`r=2` and
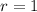`r=1`. Then the characteristic solution is

`\boxed{y = C_1 e^(2x) + C_2 e^x}`

By substituting
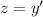`z = y'` and
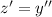`z' = y''`, the ODE transforms to

`(dz)/(dx) - 3z + 2y = 0`

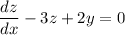
so we have the system of ODEs

`\begin{cases} z' = 3z - 2y \\ y' = z \end{cases}`

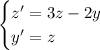
In matrix form,

`\frac d{dx} \begin{bmatrix} z \\ y \end{bmatrix} = \begin{bmatrix} 3 & -2 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} z \\ y \end{bmatrix}`

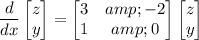
Compute the eigenvalues of the coefficient matrix.

`\begin{vmatrix} 3 - \lambda & -2 \\ 1 & -\lambda \end{vmatrix} = \lambda^2 - 3\lambda + 2 = (\lambda - 2) (\lambda - 1) = 0 \\\\ \implies \lambda = 2 \text{ or } \lambda = 1`

Compute the corresponding eigenvectors.

`\lambda = 2 \implies \begin{bmatrix} 1 & -2 \\ 1 & -2 \end{bmatrix} \vec v = \vec 0 \implies \vec v = \begin{bmatrix}2 \\ 1\end{bmatrix}`

`\lambda = 1 \implies \begin{bmatrix}2 & -2 \\ 1 & -1 \end{bmatrix} \vec v = \vec 0 \implies \vec v = \begin{bmatrix}1 \\ 1 \end{bmatrix}`

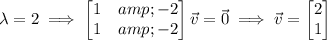
Then the characteristic solution to the system is

`\begin{bmatrix} z \\ y \end{bmatrix} = C_1 e^(2x) \begin{bmatrix} 2 \\ 1 \end{bmatrix} + C_2 e^x \begin{bmatrix}1 \\ 1 \end{bmatrix}`

but we only want the second component,

`\boxed{y = C_1 e^(2x) + C_2 e^x}`

You also mention "initial value problem" but it's unclear what the initial values are. It looks like you might have meant
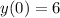`y(0)=6` and
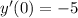`y'(0) = -5`, in which case

`y(0) = C_1 + C_2 = 6`

`y'(0) = 2C_1 + C_2 = -5`

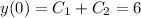
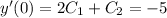
By elimination,

`(C_1 + C_2) - (2C_1 + C_2) = 6 - (-5) \implies -C_1 = 11 \\\\ \implies C_1 = -11 \text{ and } C_2 = 17`

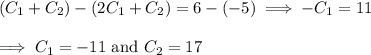
and so the particular solution is

`y = -11 e^(2x) + 17 e^x`

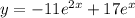
You did write d2y/dx2=-5, though, so you also could have meant
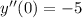`y''(0) = -5`, n which case

`y(0) = C_1 + C_2 = 6`

`y''(0) = 4C_1 + C_2 = -5`

`\!\!\implies (C_1 + C_2) - (4C_1 + C_2) = 6 - (-5) \implies -3C_1 = 11\\\\ \implies C_1 = -\frac{11}3 \text{ and } C_2 = \frac{29}3`

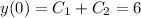
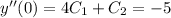
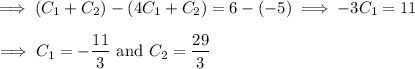
Take your pick.