Question

There’s a competition with 6 people. 3 of the 6 advance to the next round. 3 of the 6 are representing the same team. What’s the percentage chance of the previously mentioned team advancing at least one person?

Answer 1

The percentage of at least one person of the team advanced is 95%

Explanation:

For this exercise is necessary to understand the concept of combination, this is calculate as:

`nCk=(n!)/(k!(n-k)!)`

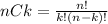
Where n is the total elements and k is the size of the group that is going to be chosen. This calculation give as the number of ways that is possible to choose a group of k with n elements.

So, the only possibility that there is no one of the same team that advance to the next round is that all of the people chosen were of the other 3 that doesn’t belong to the group mentioned. Then there is only one way to get this case.

On the other hand there are 20 ways to conform a group of 3 from a 6 elements and is calculate as:

`6C3=(6!)/(3!(6-3)!)`

`6C3=20`

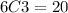
Therefore, the percentage that any of the group mentioned pass to the next round is 1 in 20 or 5%.

So, the percentage that at least one of the group mentioned pass to the next round is the compliment, that’s mean that it is 95%.