Question

Is (2,10)(4,9)(6,8)(8,7) linear?
if not, why?

Answer 1

Yes because no matter what two points you choose to calculate the rate of change (the slope), you get the same result.

Explanation:

If it is linear, then it shouldn't matter what two points I use to calculate the rise to run (slope).

The slope formula given two points is:

`(y_2-y_1)/(x_2-x_1)`.

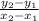We need to see if this equation holds. That is we want to see if we get the same value per each fraction:

`(10-9)/(2-4)=(9-8)/(4-6)=(8-7)/(6-8)`

`(1)/(-2)=(1)/(-2)=rac{1}{-2}`

`-.5=-.5=-.5`

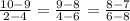
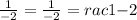
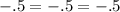
I did not move anything from one side to another.

I just simplified each fraction to see if I would get the same value and I did.

The slope is -.5, so it is a line.

We can also see what happens when we graph it. It should appear to be forming a line.

Now you could also find the equation using two points and see if the other points satisfy the equation.

So if you followed the patter of the first two points which is right twice and down once you could find the y-intercept by going up once and right twice from (2,10) which puts you at (0,11).

The y-intercept is (0,11) and we already calculated the slope from the first 2 points which was -1/2 or -.5.

But lets do it again. The slope can be found by lining up the points and subtracting vertically and then put 2nd difference over 1st difference.

Like so:

( 2 , 10)

-( 4 , 9)

-------------

-2 1

So the slope is -1/2 or -0.5.

The equation for the line is y=(-1/2)x+11

Let's check it for our points:

(2,10)?

10=(-1/2)(2)+11

10=-1+11

10=10 is true so (2,10) is on the line y=(-1/2)x+11.

(4,9)?

9=(-1/2)(4)+11

9=-2+11

9=9 is true so (4,9) is on the line y=(-1/2)x+11.

(6,8)?

8=(-1/2)(6)+11

8=-3+11

8=8 is true so (6,8) is on the line y=(-1/2)x+11.

(8,7)?

7=(-1/2)(8)+11

7=-4+11

7=7 is true so (8,7) is on the line y=(-1/2)x+11.

So all the points are on the same line. So the set of points is linear.