Question

Toys-A-Go makes toys at Plant A and Plant B. Plant A needs to make a minimum of 1000 toy dump trucks and fire engines. Plant B needs to make a minimum of 800 toy dump trucks and fire engines. Plant A can make 10 toy dump trucks and 5 toy fire engines per hour. Plant B can produce 5 toy dump trucks and 15 toy fire engines per hour. It costs $30 per hour to produce toy dump trucks and $35 per hour to operate produce toy fire engines. How many hours should be spent on each toy in order to minimize cost? What is the minimum cost?

Answer 1

88 hours on dump truck

24 hours on fire engine

Minimum cost is $3480

Explanation:

D > 0; f >0

Plant A : 10d+5f >100

Plant B: 5d +15f >800

Cost:

C(x,y)+30D+35F

Answer 2

88 hours on dump truck and 24 hours on fire engine.

The minimum cost will be $3480.

Explanation:

Constraints will be :

`d\geq 0 ; f\geq 0`

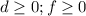
Plant A:

`10d+ 5f \geq1000`

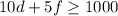
Plant B:

`5d+15f \geq 800`

The Cost function is given as:

`C=30d+35f`

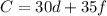
Now graphing this we will get the points (0,200) , (88,24) , (160,0)

So, the answer would be 88 hours on dump truck and 24 hours on fire engine.

And cost will be :

`C=30(88)+35(24)`

=
`C=2640+840`

= $3480