Answer:
distance between seats = 2*11.10 = 22.20 m
Step-by-step explanation:
seats row is parallel to a stage with a distance d = 90 m
doorway width = 0.070 m
speaker frequency = 4.00 * 10^4 Hz
Speed of sound = 343 m/s
tone will be heard at
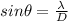
we know that

so

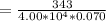
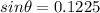
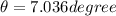
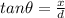
[tex]x = d*tan\theta = 90*0.1234 = 11.10 m
distance between seats = 2*11.10 = 22.20 m