Answer:
The particle takes 3.41 sec to reach 100 ft.
Step-by-step explanation:
Given that,
Velocity v= 2s+1
Distance s = 100 ft
Acceleration :
The acceleration is the first derivative of the velocity of the particle.
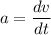
But,
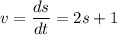
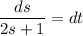
Multiply by 2 in both side
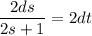
On integrating both side
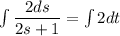
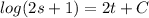
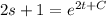
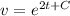
On differentiating w.r.to t
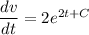
The acceleration at s = 3
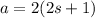
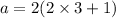
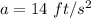
(II). We need to calculate the time
Using equation of motion
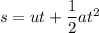 ....(II)
....(II)
We need to calculate the initial velocity
The particle's velocity is
v= 2s+1
Put the value of s in the equation
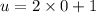
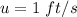
Now, Put the value in the equation (II)
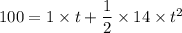
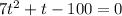
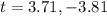
t can not be negative.
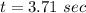
Hence, The particle takes 3.41 sec to reach 100 ft.