Question

Three kilograms of steam is contained in a horizontal, frictionless piston and the cylinder is heated at a constant pressure of 0.5 bar from 100 °C to such a temperature that the specific volume increases by 2.5 times. If the amount of heat that must be added to accomplish this change is 500 kJ, calculate the final temperature of the steam, the expansion work, and the change in internal energy.

Answer 1

Final temperature: 659.8ºC

Expansion work: 3*75=225 kJ

Internal energy change: 275 kJ

Step-by-step explanation:

First, considering both initial and final states, write the energy balance:

`U_(2)-U_(1)=Q-W`

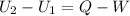
Q is the only variable known. To determine the work, it is possible to consider the reversible process; the work done on a expansion reversible process may be calculated as:

`dw=Pdv`

The pressure is constant, so:
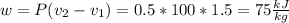`w=P(v_(2)-v_(1) )=0.5*100*1.5=75(kJ)/(kg)` (There is a multiplication by 100 due to the conversion of bar to kPa)

So, the internal energy change may be calculated from the energy balance (don't forget to multiply by the mass):

`U_(2)-U_(1)=500-(3*75)=275kJ`

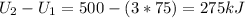
On the other hand, due to the low pressure the ideal gas law may be appropriate. The ideal gas law is written for both states:

`P_(1)V_(1)=nRT_(1)`

`P_(2)V_(2)=nRT_(2)\\V_(2)=2.5V_(1)\\P_(2)=P_(1)\\2.5P_(1)V_(1)=nRT_(2)`

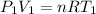
Subtracting the first from the second:

`1.5P_(1)V_(1)=nR(T_(2)-T_(1))`

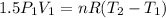
Isolating
`T_(2)`:

`T_(2)=T_(1)+(1.5P_(1)V_(1))/(nR)`

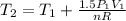
Assuming that it is water steam, n=0.1666 kmol

`V_(1)=(nRT_(1))/(P_(1))=(8.314*0.1666*373.15)/(500) =1.034m^(3)`

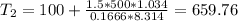`T_(2)=100+(1.5*500*1.034)/(0.1666*8.314)=659.76` ºC