Question

The name of the lesson is "Using Trigonometric Laws" The two non-parallel sides of an isosceles trapezoid are each 7 feet long. The longer of the two bases measures 22 feet long. The sum of the base angles is 140°. a. Find the length of the diagonal. b. Find the length of the shorter base. Round your answers to the nearest hundredth.

Answer 1

diagonal is 20.68 ft; shorter base is 17.21 ft

Explanation:

If base angles add up to 140, then each is 70 since this is an isosceles trapezoid. We can use the Law of Cosines now to find the length of the diagonal which I will call d:

`d^2=7^2+22^2-2(7)(22)cos(70)` and

`d^2=533-308cos(70)` and

`d^2=533-105.3422041`,

`d^2=427.6577959`

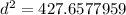
so the length of the diagonal is

d = 20.68 ft

The length of the shorter base is a little more tedious. First drop an altitude from each of the upper vertices to the base measuring 22 ft. We have 2 smaller right triangles now, each with unknown height (we need to find this), each with unknown base measures (we need to find this, too!), each with a base angle of 70 degrees, and each with a hypotenuse of 7. We need only work with one of these since they are both the same.

We will first find h, the height of each of these right triangles. Using the sin ratio:

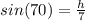`sin(70)=(h)/(7)` and

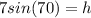`7 sin(70)=h` so

h = 6.577848

Now we can use that along with the hypotenuse measure to find the base measure, b:

`7^2-6.577848^2=b^2`,

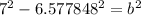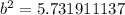`b^2=5.731911137` so

b = 2.394141002

Because we have 2 identical small right triangles with base measures of 2.394141002 each, we can subtract 2(2.394141002) from 22 to get the measure of the shorter base, which I will call x:

22 - 2(2.394141002) = x so

x = 17.21 ft