Question

At which points are the equations y=x^2+3x+2 and y=2x+3 approximately equal?

Answer 1

(0.618,4.236) and (-1.618,-0.236)

Explanation:

To find the intersection, we are looking for a common point between the curves.

We are solving the system:

`y=x^2+3x+2`

`y=2x+3`.

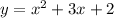
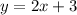I'm going to do this by substitution:

`x^2+3x+2=2x+3`

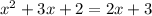
Subtract 2x and 3 on both sides:

`x^2+1x-1=0`

`x^2+x-1=0`

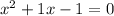
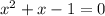
To solve this equation I'm going to use the quadratic formula:

`x=(-b\pm√(b^2-4ac))/(2a)`

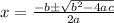
To find
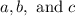`a,b,\text{ and }c`, you must compare
`x^2+x-1=0`

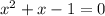
to
`ax^2+bx+c=0`.

`a=1,b=1,c=-1`.

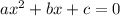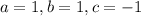Now inputting the values into the quadratic formula gives us:

`x=(-1\pm√((1)^2-4(1)(-1)))/(2(1))`

`x=(-1\pm√(1+4))/(2)`

`x=(-1\pm√(5))/(2)`

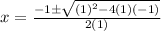
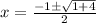
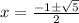
This means you have two solutions:

`x=(-1+√(5))/(2) \text{ or } x=(-1-√(5))/(2)`

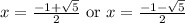
It does say approximately.

So I'm going to put both of these in my calculator and I guess round to the nearest thousandths.

`x=0.618 \text{ or } x=-1.618`

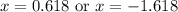
Now to find the corresponding y coordinates, I need to use one the equations along with each x.

I choose the linear equation: y=2x+3.

y=2x+3 when x=0.618

y=2(0.618)+3=4.236

So one approximate point is (0.618,4.236).

y=2x+3 when x=-1.618

y=2(-1.618)+3=-0.236

So another approximate point is (-1.618,-0.236).