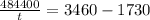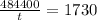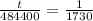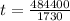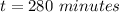Answer:
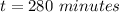
Explanation:
Let's call "v" the speed of the commercial airplane and call "t" at the travel time of the commercial plane
The distance in kilometers of the trip is: 1730 km
Then we know that:
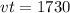
Then for the jet we have that the speed is:
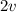
The flight time for the jet is:
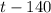
Therefore:
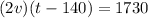
Substituting the first equation in the second we have to:
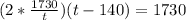
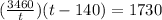
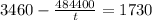
Now solve for t