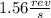Answer:
Her angular speed (in rev/s) when her arms and one leg open outward is
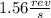
Step-by-step explanation:
Initial moment of inertia when arms and legs in is
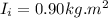
Final moment of inertia when her arms and on leg open outward,

Initial angular speed
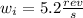
Let the final angular speed be
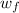
Since external torque on her is zero so we can apply conservation of angular momentum
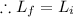
=>
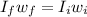
=>
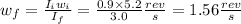
Thus her angular speed (in rev/s) when her arms and one leg open outward is