Question

Given the center of the circle (-3,4) and a point on the circle (-6,2), (10,4) is on the circle

true or false

given the center of the circle (1,3) and a point on the circle (2,6), (11,5) is on the circle

true or false ​

Answer 1

Part 1) False

Part 2) False

Explanation:

we know that

The equation of the circle in standard form is equal to

`(x-h)^(2) +(y-k)^(2)=r^(2)`

where

(h,k) is the center and r is the radius

In this problem the distance between the center and a point on the circle is equal to the radius

The formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

Part 1) given the center of the circle (-3,4) and a point on the circle (-6,2), (10,4) is on the circle.

true or false

substitute the center of the circle in the equation in standard form

`(x+3)^(2) +(y-4)^(2)=r^(2)`

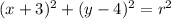
Find the distance (radius) between the center (-3,4) and (-6,2)

substitute in the formula of distance

`r=\sqrt{(2-4)^(2)+(-6+3)^(2)}`

`r=\sqrt{(-2)^(2)+(-3)^(2)}`

`r=√(13)\ units`

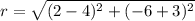
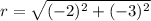
The equation of the circle is equal to

`(x+3)^(2) +(y-4)^(2)=(√(13)){2}`

`(x+3)^(2) +(y-4)^(2)=13`

Verify if the point (10,4) is on the circle

we know that

If a ordered pair is on the circle, then the ordered pair must satisfy the equation of the circle

For x=10,y=4

substitute

`(10+3)^(2) +(4-4)^(2)=13`

`(13)^(2) +(0)^(2)=13`

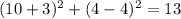
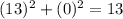
`169=13` -----> is not true

therefore

The point is not on the circle

The statement is false

Part 2) given the center of the circle (1,3) and a point on the circle (2,6), (11,5) is on the circle.

true or false

substitute the center of the circle in the equation in standard form

`(x-1)^(2) +(y-3)^(2)=r^(2)`

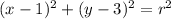
Find the distance (radius) between the center (1,3) and (2,6)

substitute in the formula of distance

`r=\sqrt{(6-3)^(2)+(2-1)^(2)}`

`r=\sqrt{(3)^(2)+(1)^(2)}`

`r=√(10)\ units`

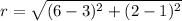
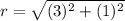
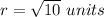
The equation of the circle is equal to

`(x-1)^(2) +(y-3)^(2)=(√(10)){2}`

`(x-1)^(2) +(y-3)^(2)=10`

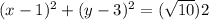
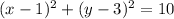
Verify if the point (11,5) is on the circle

we know that

If a ordered pair is on the circle, then the ordered pair must satisfy the equation of the circle

For x=11,y=5

substitute

`(11-1)^(2) +(5-3)^(2)=10`

`(10)^(2) +(2)^(2)=10`

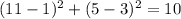
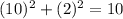
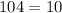`104=10` -----> is not true

therefore

The point is not on the circle

The statement is false