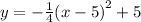1 Answer

Ohrstrom · Answer 1 · 2020-01-28T08:00:18+0000

Answer:

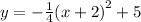
$y = - (1)/(4) {(x + 2)}^(2) + 5$

Explanation:

The vertex of this parabola is the midpoint of the focus (-2,4) and where the directrix intersects the axis of symmetry of the parabola (-2,6)

This parabola must open downwards due to the position of the directrix and has equation of the form:

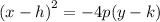
${(x - h)}^(2) = - 4p(y - k)$

where (h,k) is the vertex.

This implies that:

h = - 2

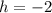
and

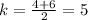
k = (4 + 6)/(2) = 5

The value of p is the distance from the vertex to the focus:

p = |6 - 5| = 1

We substitute all the values into the formula to get:

$(x - - 2)^(2) = - 4(1){(y - 5)}$

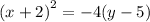
${(x + 2)}^(2) = - 4(y - 5)$

Or

$y = - (1)/(4) {(x - 5)}^(2) + 5$

Please log in or register to add a comment.