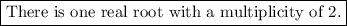Question

Examine the quadratic equation: x^2+2x+1=0

A: What is the discriminant of the quadratic equation?
B: Based on the discriminant, which statement about the roots of the quadratic equation is correct?
Select one answer choice for question A, and select one answer choice for question B.
A: 3
A: 0
A: −3
B: There is one real root with a multiplicity of 2 .
B: There are two real roots.
B: There are two complex roots

Answer 1

A: 0

B: There is one real root with a multiplicity of 2 .

Step-by-step explanation:

Given a quadratic equation:

`ax^2+bx+c=0`

You can find the Discriminant with this formula:

`D=b^2-4ac`

In this case you have the following quadratic equation:

`x^2+2x+1=0`

Where:

`a=1\\b=2\\c=1`

Therefore, when you substitute these values into the formula, you get that the discriminant is this:

`D=(2)^2-4(1)(1)\\\\D=0`

Since
`D=0`, the quadratic equation has one real root with a multiplicity of 2 .

Answer 2

A: 0

B: There is one real root with a multiplicity of 2.

Explanation:

`\bf{x^2+2x+1=0}`

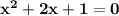
A:

The discriminant of the quadratic equation can be found by using the formula:
`b^2-4ac`.

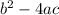In this quadratic equation,

• a = 1
• b = 2
• c = 1

I found these values by looking at the coefficient of
`x^2` and
`x`. Then I took the constant for the value of c.

Substitute the corresponding values into the formula for finding the discriminant.

• 
  `b^2-4ac`
• 
  `(2)^2-4(1)(1)`

Simplify this expression.

• 
  `(2)^2-4(1)(1)= \bf{0}`

The answer for part A is
`\boxed{0}`

B:

The discriminant tells us how many real solutions a quadratic equation has. If the discriminant is

• Negative, there are no real solutions (two complex roots).
• Zero, there is one real solution.
• Positive, there are two real solutions.

Since the discriminant is 0, there is one real root so that means that the first option is correct.

The answer for part B is
`\boxed {\text{There is one real root with a multiplicity of 2.}}`