Question

For a class activity, your group has been assigned the task of generating a quiz question that requires use of the formula for conditional probability to compute P(B | A). Your group comes up with the following question "If P(A and B) = 0.40 and P(A) = 0.20, what is the value of P(B | A)?" What is wrong with this question? Hint: Consider the answer you get when using the correct formula, P(B | A) = P(A and B)/P(A).

Answer 1

Answer: P(A and B) is greater than P(A)

P(A and B) should be smaller than P(A).

Explanation:

Given : P(A and B) = 0.40

P(A) = 0.20

Using the given formula of the conditional probability will be

`P(B|A)=\frac{\text{P(A and B)}}{P(A)}\\\\=(0.40)/(0.20)=2`

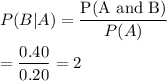
But we know that the probability of any event cannot be more than 1.

Also, the probability of the intersection must be less than the probability of individual event.

Thus , in the given question P(A and B) must be smaller than P(A).