Answer:
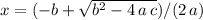 or
or
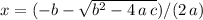 assuming that
assuming that
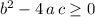 .
.
Explanation:
Let
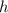 and
and
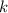 be constants. Consider
be constants. Consider
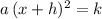 . In this equation,
. In this equation,
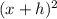 , the only term that includes
, the only term that includes
 , is a perfect square. If
, is a perfect square. If
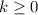 , solving this equation is as simple as taking the square root of both sides of the equation:
, solving this equation is as simple as taking the square root of both sides of the equation:
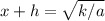 or
or
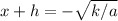 .
.
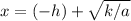 or
or
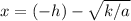 .
.
Assume that there are values for
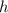 and
and
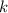 such that
such that
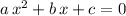 is equivalent to
is equivalent to
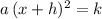 . If
. If
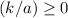 , then
, then
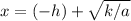 and
and
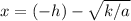 would be solutions to
would be solutions to
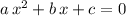 .
.
Apply binomial expansion to
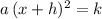 and rewrite to find the values for
and rewrite to find the values for
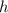 and
and
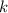 :
:
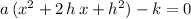 .
.
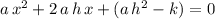 .
.
Match the coefficients of this equation with those in
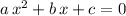 :
:
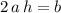 .
.
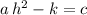 .
.
Solve for
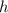 and
and
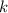 in terms of
in terms of
 ,
,
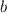 , and
, and
 :
:
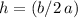 .
.
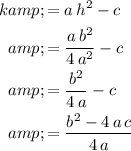 .
.
Hence, as long as
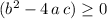 , (such that
, (such that
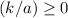 ,) solutions to
,) solutions to
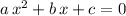 would be:
would be:
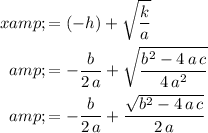 , and
, and
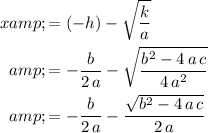 .
.