Answer:
The initial number of bacteria is 371.
Step-by-step explanation:
Let P represents population of the bacteria and t represents time,
According to the question,

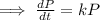
Where, k is constant of proportionality,
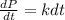
Integrating both sides,
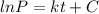

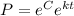
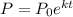 ( Let
( Let
 )
)
If t = 0,
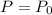
That is,
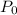 is the intial population.
is the intial population.
Since, when t = 3, P = 500 and when t = 10, P=4000
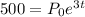
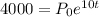
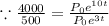
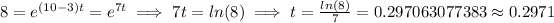
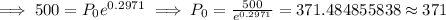
Hence, initial population is approximately 371.