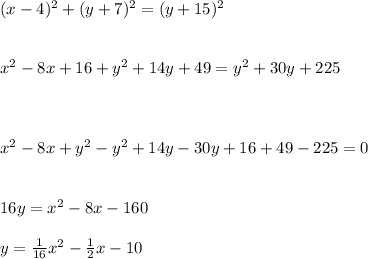Question

Derive the equation of the parabola with a focus at (4, −7) and a directrix of y = −15. Put the equation in standard form. (2 points) Question 5 options: 1) f(x) = one sixteenth x2 − 8x + 11 2) f(x) = one sixteenth x2 − 8x − 10 3) f(x) = one sixteenth x2 − x + 11 4) f(x) = one sixteenth x2 − x − 10

Answer 1

`(1)/(16) x^2-(1)/(2) x-10`

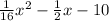
Explanation:

When (x,y) is a point on the parabola, the distance from the focus is equal to its distance from the directrix.

Given point as (4,-7) and directrix as y=-15 then;

distance to focus=distance to directrix

Apply formula for distance

`√((x-4)^2+(y+7)^2) =(y+15)`

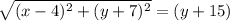
square both sides

`(x-4)^2+(y+7)^2=(y+15)^2\\\\\\x^2-8x+16+y^2+14y+49=y^2+30y+225\\\\\\\\x^2-8x+y^2-y^2+14y-30y+16+49-225=0\\\\\\16y=x^2-8x-160\\\\y=(1)/(16) x^2-(1)/(2) x-10`