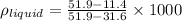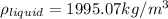Question

A rock is suspended by a light string. When the rock is in air, the tension in the string is 51.9 N . When the rock is totally immersed in water, the tension is 31.6 N . When the rock is totally immersed in an unknown liquid, the tension is 11.4 N. What is the Density of the unknown liquid. -When I looked at this problem, I though we needed to know the volume of the rock. Can someone show me how to do it without the volume of this rock?

Answer 1

`\rho _(liquid)=1995.07kg/m^(3)`

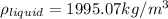
Step-by-step explanation:

When the rock is immersed in unknown liquid the forces that act on it are shown as under

1) Tension T by the string

2) Weight W of the rock

3) Force of buoyancy due to displaced liquid B

For equilibrium we have
`T_(3)+B = W_(rock)`

`T_(3)+\rho _(Liquid)V_(rock)g`=
`W_(rock).....(\alpha)`

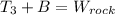
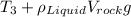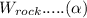
When the rock is suspended in air for equilibrium we have

`T_(1)=W_(rock)....(\beta)`

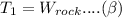
When the rock is suspended in water for equilibrium we have

`T_(2)` +
`\rho _(water)V_(rock)g`=
`W_(rock).....(\gamma)`

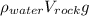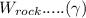
Using the given values of tension and solving α,β,γ simultaneously for
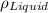`\rho _(Liquid)` we get

`W_(rock)=51.9N\\31.6+1000* V_(rock)* g=51.9N\\\\11.4+\rho _(liquid)V_(rock)g=51.9N\\\\`

Solving for density of liquid we get

`\rho _(liquid)=(51.9-11.4)/(51.9-31.6)* 1000`

`\rho _(liquid)=1995.07kg/m^(3)`