Answer:
The point which lie on the circle is :
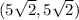
Explanation:
It is given that the circle is centered at origin and has a radius of 10 units.
We know that if (h, k) represents the coordinate of the center of circle and r is the radius of the circle then the equation of circle is given by:

Here we have:
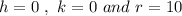
Hence, the equation of circle is given by:
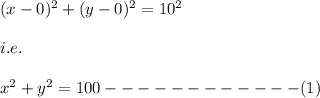
If we substitute the given point into the equation of the circle and it makes the equation true then the point lie on the circle and if it doesn't make the equation true then the point do not lie on the circle.
a)
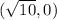
i.e.
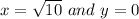
i.e. we put these points in the equation(1)

which is a false statement .
Hence, this point do not lie on the circle.
b)
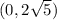
i.e.
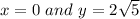
i.e. we put these points in the equation(1)
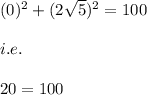
which is a false statement .
Hence, this point do not lie on the circle.
c)
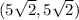
i.e.
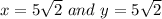
i.e. we put these points in the equation(1)
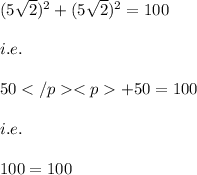
which is a true statement .
Hence, this point lie on the circle.