Answer:
Option C
Explanation:
In this question coordinates of rhombus WXYZ are given as W(0, 4b), X(2a, 0), Y(0, −4b), and Z(−2a, 0).
Now we have to find the coordinates of midpoint of WZ as part of the proof.
Since mid point of two points (x, y) and (x', y') is represented by
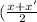
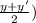
For midpoint of WZ,
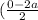

= (-a, 2b)
Option C will be the answer.