Answer:
Part 1) The value that is closest to the cost of finishing a sphere with a 5.50-meter circumference is $900
Part 2) The value that is closest to the cost of finishing a sphere with a 7.85-meter circumference is $1,800
Explanation:
Step 1
Find the radius of each sphere
we know that
The circumference of a circle is equal to
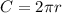
Find the radius of the sphere with a 5.50-meter circumference
For
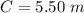
assume
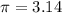
substitute and solve for r
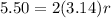
![r=5.50/[2(3.14)]=0.88\ m](https://img.qammunity.org/2020/formulas/mathematics/high-school/jncok40hj6x7azelxi36d1gv08y6q2986y.png)
Find the radius of the sphere with a 7.85-meter circumference
For
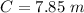
assume
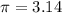
substitute and solve for r

![r=7.85/[2(3.14)]=1.25\ m](https://img.qammunity.org/2020/formulas/mathematics/high-school/58whu9v1le92ixegzlv4b7qpf48lhc47uq.png)
step 2
Find the surface area of each sphere
The surface area of sphere is equal to
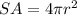
Find the surface area of sphere with a 5.50-meter circumference
For
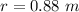
assume
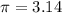
substitute
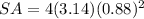
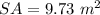
Find the surface area of sphere with a 7.85-meter circumference
For
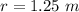
assume
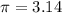
substitute
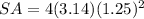
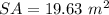
step 3
Find the cost of finishing each sphere
we know that
To find out the cost , multiply the surface area by $92 per square meter
Find the cost of sphere with a 5.50-meter circumference
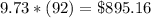
therefore
The value that is closest to the cost of finishing a sphere with a 5.50-meter circumference is $900
Find the cost of sphere with a 7.85-meter circumference
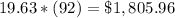
therefore
The value that is closest to the cost of finishing a sphere with a 7.85-meter circumference is $1,800