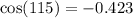Answer:
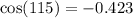
Explanation:
The parametric equations of a circle is
 and
and
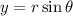
The radius of the unit circle is 1 unit.
This implies that any point on the unit circle is represented by:
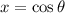 and
and
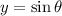
where
 is the angle in standard position,
is the angle in standard position,
From the question, the given angle in standard position is
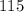 .
.
This angle intersects the unit circle at
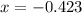
But
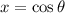
We substitute
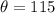 and
and
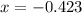
This implies that: