Answer:
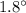
Step-by-step explanation:
The diffraction angles
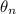 when we have a slit divided into
when we have a slit divided into
 parts are obtained by the following equation:
parts are obtained by the following equation:
 (1)
(1)
Where:
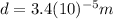 is the width of the slit
is the width of the slit
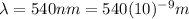 is the wavelength of the light
is the wavelength of the light
 is an integer different from zero.
is an integer different from zero.
Now, the second-order diffraction angle is given when
 , hence equation (1) becomes:
, hence equation (1) becomes:
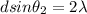 (2)
(2)
Now we have to find the value of
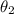 :
:
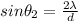 (3)
(3)
Then:
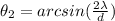 (4)
(4)
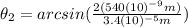 (5)
(5)
Finally:
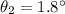 (6)
(6)