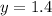Question

-y varies inversely with x. When y = 9.6, x = 12. What is the value of k, the constant of inverse variation?

Round to the nearest tenth, if necessary.


-y varies inversely with x, and k (the constant of variation) = 5.6. What is the value of y when x = 4?

Round to the nearest tenth, if necessary

Answer 1

Question 1:

For this case we have an equation of the form:

`y = \frac {k} {x}`

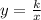
Where,

• k: inverse variation constant.

Then, substituting values we have:

`y =\frac {k} {x}`

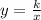
From here, we clear the value of k.

We have then:

`k = 9.6 * 12\\k = 115.2`

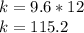
Answer:

the constant of inverse variation is:

`k = 115.2`

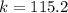
Question 2:

For this case we have:

`y = \frac {k} {x}`

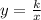
Where,

• k: constant of variation.

Then, substituting the value of the constant we have:

`y =\frac {5.6} {x}`

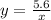
We now substitute the value of x:

`y = \frac {5.6} {4}\\y = 1.4`

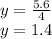
Answer:

the value of y when x = 4 is:
`y = 1.4`