It depends on what method you're using to approximate. Newton's method is a popular choice. Let
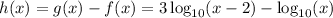 , with derivative
, with derivative
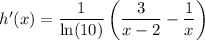
which follows from
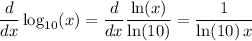
Judging by the plots, we have
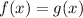 for some
for some
 between 3 and 4. So let's take an initial approximation of
between 3 and 4. So let's take an initial approximation of
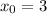 . Newton's method involves taking the tangent line approximation to
. Newton's method involves taking the tangent line approximation to
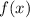 at
at
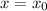 , then using the
, then using the
 -intercept of this tangent line as the next approximation,
-intercept of this tangent line as the next approximation,
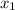 .
.
The linear approximation at
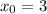 is
is
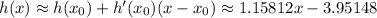
with intercept at
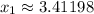 .
.
Repeat until you reach the desired threshold of accuracy. The next linear approximation at
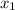 is
is
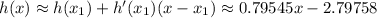
with intercept
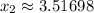 .
.
The next approximation at
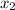 is
is
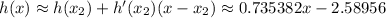
with intercept
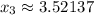 .
.
And so on. The actual solution has an approximate value of about
3.521379706804567569604081
so after just 3 approximations we're already less than
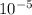 away.
away.