Question

Calculating cos-1 ( help is gladly appreciated :) )

Answer 1

`(3\pi)/(4)`

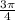
(Assuming you want your answer in radians)

If you want the answer in degrees just multiply your answer in radians by
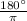`(180^\circ)/(\pi)` giving you:

`(3\pi)/(4) \cdot (180^\circ)/(\pi)=(3(180))/(4)=135^(\circ)`.

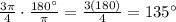We can do this since
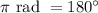`\pi \text{ rad }=180^\circ` (half the circumference of the unit circle is equivalent to 180 degree rotation).

Explanation:

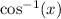`\cos^(-1)(x)` is going to output an angle measurement in
`[0,\pi]`.

So we are looking to solve the following equation in that interval:

`\cos(x)=-(√(2))/(2)`.

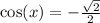This happens in the second quadrant on the given interval.

The solution to the equation is
`(3\pi)/(4)`.

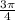So we are saying that
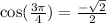`\cos((3\pi)/(4))=(-√(2))/(2)` implies
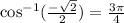`\cos^(-1)((-√(2))/(2))=(3\pi)/(4)` since
`(3\pi)/(4) \in [0,\pi]`.

Answer is
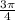`(3\pi)/(4)`.