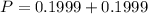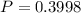Answer:
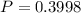
Explanation:
Let
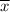 be the average of the sample, and the population mean will be
be the average of the sample, and the population mean will be

We know that:
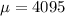 gr
gr
Let
 be the standard deviation and n the sample size, then we know that the standard error of the sample is:
be the standard deviation and n the sample size, then we know that the standard error of the sample is:
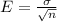
Where
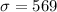
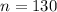
In this case we are looking for:

This is:
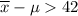 or
or
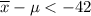
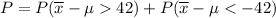
Now we get the z score
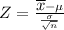
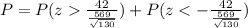
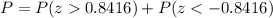
Looking at the tables for the standard nominal distribution we get