Question

There are 6 people in a raffle drawing, Two raffle winners each win gift cards,

Each gift card is the same. How many ways are there to choose the winners?
Decide if the situation involves a permutation or a combination, and then find
the number of ways to choose the winners.

Answer 1

b

Explanation:

apeex

Answer 2

B. Combination: Number of ways = 15

Explanation:

2 winners are to be chosen out of 6 people participating in the raffle drawing. In this case the order of selection does not matter, therefore, this situation involves combinations

So, we have to find combinations of 6 people taken 2 at a time. This can be represented by 6C2. The general formula for combinations is:

`^(n)C_(r)=(n!)/(r!(n-r)!)`

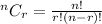
In this case n = 6 and r = 2. Using these values, we get:

`^(6)C_(2)=(6!)/(2! * (6-2)!) \\\\ ^(6)C_(2)= (6!)/(2! * 4!)\\\\ ^(6)C_(2)=(6 * 5 * 4!)/(2 * 4!)\\\\ ^(6)C_(2)= (30)/(2)\\\\ ^(6)C_(2)= 15`

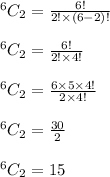
Thus, there are 15 ways to chose the winners. So, option B gives the correct answer.