Question

I need help with letters (D) and (E). My model equation from letter (C) is: P = -55/4 t+ 340.

Answer 1

(a) The two ordered pairs are (0 , 340) and (4 , 285)

(b) The slope is m = -55/4

The slope means the rate of decreases of the owl population was 55/4

per year (P decreased by 55/4 each year)

(c) The model equation is P = -55/4 t + 340

(d) The owl population in 2022 will be 216

(e) At year 2038 will be no more owl in the park

Explanation:

* Lets explain how to solve the problem

- The owl population in 2013 was measured to be 340

- In 2017 the owl population was measured again to be 285

- The owl population is P and the time is t where t measure the numbers

of years since 2013

(a) Let t represented by the x-coordinates of the order pairs and P

represented by the y-coordinates of the order pairs

∵ t is measured since 2013

∴ At 2013 ⇒ t = 0

∵ The population P in 2013 was 340

∴ The first order pair is (0 , 340)

∵ The time from 2013 to 2013 = 2017 - 2013 = 4 years

∴ At 2017 ⇒ t = 4

∵ The population at 2017 is 285

∴ The second order pair is (4 , 285)

* The two ordered pairs are (0 , 340) and (4 , 285)

(b) The slope of any lines whose endpoints are (x1 , y1) and (x2 , y2)

is
`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

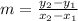
∵ (x1 , y1) is (0 , 340) and (x2 , y2) is (4 , 285)

∴ x1 = 0 , x2 = 4 and y1 = 340 , y2 = 285

∴
`m = (285-340)/(4-0)=(-55)/(4)`

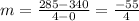
* The slope is m = -55/4

∵ The slope is negative value

∴ The relation is decreasing

* The slope means the rate of decreases of the owl population was

55/4 per year (P decreased by 55/4 each year)

(c) The linear equation form is y = mx + c, where m is the slope and c is

the value of y when x = 0

∵ The population is P and represented by y

∵ The time is t and represented by t

∴ P = mt + c , c is the initial amount of population

∵ m = -55/4

∵ The initial amount of the population is 340

∴ P = -55/4 t + 340

* The model equation is P = -55/4 t + 340

(d) Lets calculate the time from 2013 to 2022

∵ t = 2022 - 2013 = 9 years

∵ P = -55/4 t + 340

∴ P = -55/4 (9) + 340 = 216.25 ≅ 216

* The owl population in 2022 will be 216

(e) If the model is accurate , then the owl population be be zero after

t years

∵ P = -55/4 t + 340

∵ P = 0

∴ 0 = -55/4 t + 340

- Add 55/4 t to both sides

∴ 55/4 t = 340

- Multiply both sides by 4

∴ 55 t = 1360

- Divide both sides by 55

∴ t = 24.7 ≅ 25 years

- To find the year add 25 years to 2013

∵ 2013 + 25 = 2038

* At year 2038 will be no more owl in the park