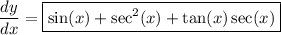d) By the product rule,
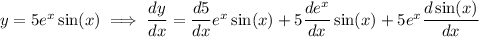
The derivative of a constant is 0; the derivative of
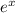 is
is
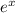 ; the derivative of
; the derivative of
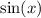 is
is
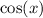 . So
. So
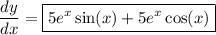
e) Rewrite
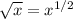 . By the product rule,
. By the product rule,
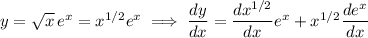
By the power rule,

Then
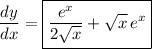
f) By the product rule,

The derivative of
 is
is
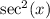 . So
. So
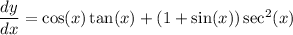
which we can simplify using
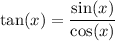
and expand to get