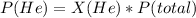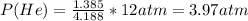Answer:
The partial pressure of He = 3.97 atm
Step-by-step explanation:
Given:
Mass of CO2 = 35.07 g
Mass of H2O = 27.93 g
Mass of N2 = 12.64 g
Mass of He = 5.54 g
Total pressure P = 12 atm
To determine:
The partial pressure of He
Calculation:
Based on Dalton's law, the partial pressure of a gas can be expressed as a product of its mole fraction and the total pressure
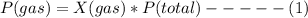
where X(gas) = mole fraction
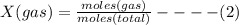
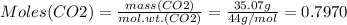
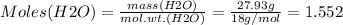
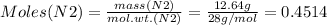
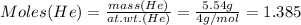
Therefore:
Moles of He = 1.385
Total moles = 0.7970+1.552+0.4514+1.385 =4.188
Substituting the appropriate values in equation (1) gives: