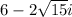Question

The sum of two numbers is 12, their product is 96. Compute these two numbers. Explain.​

Answer 1

The numbers are

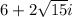`6+2√(15)i` and
`6-2√(15)i`

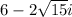
Explanation:

Let

x and y -----> the numbers

we know that

`x+y=12` ----->
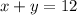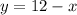`y=12-x` ------> equation A

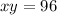`xy=96` ----> equation B

substitute equation A in equation B and solve for x

`x(12-x)=96\\12x-x^(2)=96\\x^(2) -12x+96=0`

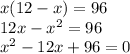
Solve the quadratic equation

The formula to solve a quadratic equation of the form
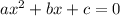`ax^(2) +bx+c=0` is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

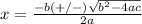
in this problem we have

`x^(2) -12x+96=0`

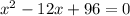
so

`a=1\\b=-12\\c=96`

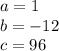
substitute

`x=\frac{-(-12)(+/-)\sqrt{-12^(2)-4(1)(96)}} {2(1)}`

`x=\frac{12(+/-)√(-240)} {2}`

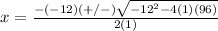
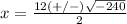
Remember that

`i^(2)=√(-1)`

`x=\frac{12(+/-)√(240)i} {2}`

`x=\frac{12(+/-)4√(15)i} {2}`

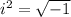
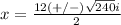
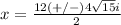
Simplify

`x=6(+/-)2√(15)i`

`x1=6+2√(15)i`

`x2=6-2√(15)i`

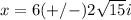
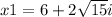
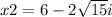
we have two solutions

Find the value of y for the first solution

For
`x1=6+2√(15)i`

`y=12-x`

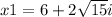
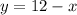
substitute

`y1=12-(6+2√(15)i)`

`y1=6-2√(15)i`

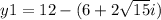
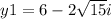
Find the value of y for the second solution

For
`x2=6-2√(15)i`

`y2=12-x`

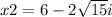
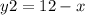
substitute

`y2=12-(6-2√(15)i)`

`y2=6+2√(15)i`

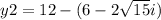
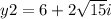
therefore

The numbers are

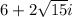`6+2√(15)i` and
`6-2√(15)i`